Lai Tat Hei (Teddy)

Lai Tat Hei (Teddy)

Bachelor of Electronic and Information Engineering, The Hong Kong Polytechnic University

Navigation coordinate system and transformation relationship

2 minute read

Published:

  1. Introduction
    In this blog, I will talk about the most common navigation coordinate system (frame) used in application level with code implementation. The reference book for this blog is Fundamentals of Inertial Navigation, Satellite-based Positioning and their Integration and Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems

  2. Earth-Centered Earth-Fixed Frame (ECEF frame)
    ECEF frame share the same origin and z-axis as the ECI frame (Earth-Centered Inertial Frame), but the main difference between these two navigation frame is ECEF frame rotates along with the Earth. In application level, most of the GNSS default data will follow ECEF frame, which means it provided latitude, longitude, altitude data in ECEF frame. Therefore, most people will use LLA as short forms to describe latitude, longitude, altitude data, but they are actually refering to ECEF frame.


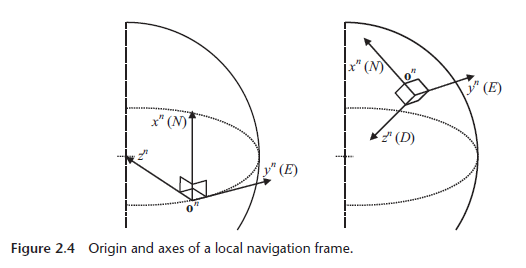
  3. Local-Level Frame (LLF frame)
    LLF frame aim to represent a vehicle’s attitude and velocity when on or near the surface of the Earth. Sometimes, people will also call this frame as local geodetic or navigation frame. Also, there are two kind of coordinate representations which are NED (north, east and down) and ENU (east, north and up) to describe xyz position order.


  4. World Geodetic System (WGS)
    As the earth is not perfect sphere, many scientists spend a lot of effort figuring out the parameters and equations best suited to approximate the shape of the Earth. In application level, most people will use WGS84 in calculation.
    a = 6378137.0  # equatorial radius / semimajor axis (m)
b = 6356752.3142 # polar radius / semiminor axis (m)
f = 0.00335281066 # flattening
e = 0.08181919 # Eccentricity
e_square = e**2
gm = 3.986004418E14  # Gravitational constant (m^3/s^2)
omega_ie = 7.2921151467E-05  # Earth rotation rate (rad/s)


  5. Code Example

    There are some code samples to demonstrate coordinate transformation. 
def lla2ecef(lat,lon,alt):
    lat = np.deg2rad(lat) 
    lon = np.deg2rad(lon)
    N = a / np.sqrt(1 - e**2 * np.sin(lat)**2)
    x = (N + alt) * np.cos(lat) * np.cos(lon)
    y = (N + alt) * np.cos(lat) * np.sin(lon)
    z = (N * (1 - e**2) + alt) * np.sin(lat)
    return x, y, z

def lla2enu(lat,lon,alt,lat_ref,lon_ref,alt_ref): # those lla in degrees
    # Convert from LLA to ECEF
    x, y, z = lla2ecef(lat,lon,alt)
    x_ref, y_ref, z_ref = lla2ecef(lat_ref,lon_ref,alt_ref)

    # Convert from ECEF to ENU
    cur = np.array([x, y, z])
    ref = np.array([x_ref, y_ref, z_ref])
    d = cur-ref
    lat_ref = np.deg2rad(lat_ref) 
    lon_ref = np.deg2rad(lon_ref)
    rotation_matrix = np.array([[-np.sin(lon_ref), np.cos(lon_ref), 0],
                                [-np.sin(lat_ref)*np.cos(lon_ref), -np.sin(lat_ref)*np.sin(lon_ref), np.cos(lat_ref)],
                                [np.cos(lat_ref)*np.cos(lon_ref), np.cos(lat_ref)*np.sin(lon_ref), np.sin(lat_ref)]])

    point_enu = np.dot(rotation_matrix, d)
    return point_enu # return the local cartesian position

You May Also Enjoy