Point in Polygon
Published:
- Define Problem
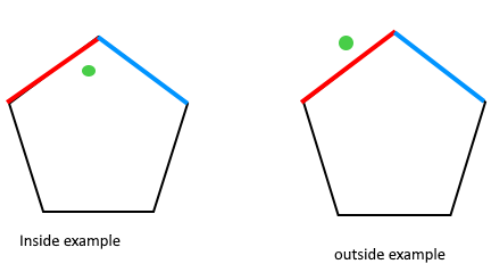
The problem of points in polygons is a very classical geometric problem.
The ray casting algorithm is one of the algorithms to solve it.
Algorithm explaination

Draw a horizontal line to the right of each point and extend it to infinity
Count the number of times the line intersects with polygon edges.
A point is inside the polygon if either count of intersections is odd or point lies on an edge of polygon. If none of the conditions is true, then point lies outside.Code implementation
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
struct Point {
double x, y;
};
// Checking if a point is inside a polygon
bool point_in_polygon(Point point, vector<Point> polygon) {
int num_vertices = polygon.size();
double x = point.x, y = point.y;
bool inside = false;
// Store the first point in the polygon and initialize the second point
Point p1 = polygon[0], p2;
// Loop through each edge in the polygon
for (int i = 1; i <= num_vertices; i++) {
// Get the next point in the polygon
p2 = polygon[i % num_vertices];
// Check if the point is above the minimum y coordinate of the edge
if (y > min(p1.y, p2.y)) {
// Check if the point is below the maximum y coordinate of the edge
if (y < max(p1.y, p2.y)) {
// Check if the point is to the left of the maximum x coordinate of the edge
if (x < max(p1.x, p2.x)) {
/*
Calculate the x-intersection of the line connecting the point to the edge
*/
double x_intersection = (y - p1.y) * (p2.x - p1.x) / (p2.y - p1.y) + p1.x;
// Check if the point is on the same line as the edge or to the left of the x-intersection
if (p1.x == p2.x || x <= x_intersection) {
// Flip the inside flag
inside = !inside;
}
}
}
}
// Store the current point as the first point for the next iteration
p1 = p2;
}
// Return the value of the inside flag
return inside;
}
