Shortest distance in 3D plane
Published:
Define Problem
Given a line passing through two points A and B and an arbitrary point C in a 3-D plane, the task is to find the shortest distance between the point C and the line passing through the points A and B.
Algorithm explaination
AB and AC and the shortest distance as CD. The Shortest Distance is always the perpendicular distance. The point D is taken on AB such that CD is perpendicular to AB.
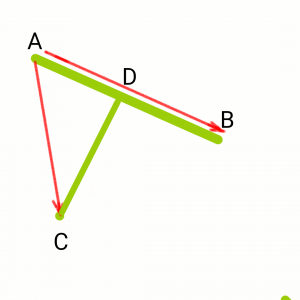
Construct BP and CP as shown in the figure to form a Parallelogram. Now C is a vertex of parallelogram ABPC and CD is perpendicular to Side AB. Hence CD is the height of the parallelogram.

The magnitude of cross product AB and AC gives the Area of the parallelogram. Also, the area of a parallelogram is Base * Height = AB * CD. So,CD = |ABxAC| / |AB|Code implementation
// C++ program to find the Shortest
// Distance Between A line and a
// Given point.
#include<bits/stdc++.h>
using namespace std;
class Vector {
private:
int x, y, z;
// 3D Coordinates of the Vector
public:
Vector(int x, int y, int z)
{
// Constructor
this->x = x;
this->y = y;
this->z = z;
}
Vector operator+(Vector v); // ADD 2 Vectors
Vector operator-(Vector v); // Subtraction
int operator^(Vector v); // Dot Product
Vector operator*(Vector v); // Cross Product
float magnitude()
{
return sqrt(pow(x, 2) + pow(y, 2) + pow(z, 2));
}
friend ostream& operator<<(ostream& out, const Vector& v);
// To output the Vector
};
// ADD 2 Vectors
Vector Vector::operator+(Vector v)
{
int x1, y1, z1;
x1 = x + v.x;
y1 = y + v.y;
z1 = z + v.z;
return Vector(x1, y1, z1);
}
// Subtract 2 vectors
Vector Vector::operator-(Vector v)
{
int x1, y1, z1;
x1 = x - v.x;
y1 = y - v.y;
z1 = z - v.z;
return Vector(x1, y1, z1);
}
// Dot product of 2 vectors
int Vector::operator^(Vector v)
{
int x1, y1, z1;
x1 = x * v.x;
y1 = y * v.y;
z1 = z * v.z;
return (x1 + y1 + z1);
}
// Cross product of 2 vectors
Vector Vector::operator*(Vector v)
{
int x1, y1, z1;
x1 = y * v.z - z * v.y;
y1 = z * v.x - x * v.z;
z1 = x * v.y - y * v.x;
return Vector(x1, y1, z1);
}
// Display Vector
ostream& operator<<(ostream& out,
const Vector& v)
{
out << v.x << "i ";
if (v.y >= 0)
out << "+ ";
out << v.y << "j ";
if (v.z >= 0)
out << "+ ";
out << v.z << "k" << endl;
return out;
}
// calculate shortest dist. from point to line
float shortDistance(Vector line_point1, Vector line_point2,
Vector point)
{
Vector AB = line_point2 - line_point1;
Vector AC = point - line_point1;
float area = Vector(AB * AC).magnitude();
float CD = area / AB.magnitude();
return CD;
}
// Driver program
int main()
{
// Taking point C as (2, 2, 2)
// Line Passes through A(4, 2, 1)
// and B(8, 4, 2).
Vector line_point1(4, 2, 1), line_point2(8, 4, 2);
Vector point(2, 2, 2);
cout << "Shortest Distance is : "
<< shortDistance(line_point1, line_point2, point);
return 0;
}
