Lai Tat Hei (Teddy)

Lai Tat Hei (Teddy)

Bachelor of Electronic and Information Engineering, The Hong Kong Polytechnic University

Line intersect polygon

1 minute read

Published:

  1. Define Problem
    Giving a line and polygon. Find out if a line intersects a polygon.

  2. Algorithm explaination
    According to the standard form of linear equation, we can simplify the equation to below which show the determinant
    If the determinant term becomes zero it means that the two line segments are parallel, otherwise they must have an intersection
    Therefore, we can find out whether a line intersects a polygon with


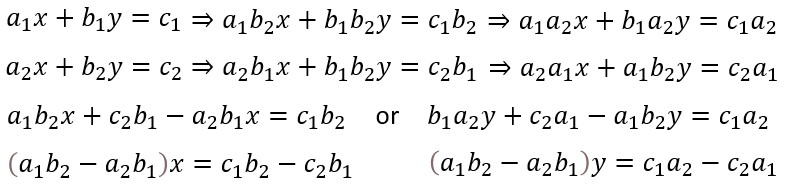
  3. Code implementation

#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

bool point_in_line(vector<vector<double>> line, vector<double> point)
{
    double distance_AC = sqrt(pow((line[0][0]-point[0]),2)+pow((line[0][1]-point[1]),2));
    double distance_BC = sqrt(pow((line[1][0]-point[0]),2)+pow((line[1][1]-point[1]),2));
    double distance_AB = sqrt(pow((line[0][0]-line[1][0]),2)+pow((line[0][1]-line[1][1]),2));
    if (distance_AC+distance_BC == distance_AB)
        return true;
    return false;
}

bool line_intersect_polygon(vector<vector<double>> segment, vector<vector<double>> polygon) 
{
    vector<double> A = segment[0]; // point 1 of the segment
    vector<double> B = segment[1]; // point 2 of the segment
    int failure = 0;
    for (int i=0;i<polygon.size()-1;i++)
    {
        vector<vector<double>> segment2 = {polygon[i],polygon[i+1]}; // one of the segment in polygon
        vector<double> C = segment2[0]; // point 1 of the polygon segment
        vector<double> D = segment2[1]; // point 2 of the polygon segment
        // Line AB represented as a1x + b1y = c1 (standard form of linear equation)
        double a1 = B[1] - A[1];
        double b1 = A[0] - B[0];
        double c1 = a1*(A[0]) + b1*(A[1]); // find out the segment equation

        // Line CD represented as a2x + b2y = c2 (standard form of linear equation)
        double a2 = D[1] - C[1];
        double b2 = C[0] - D[0];
        double c2 = a2*(C[0])+ b2*(C[1]); // find out the polygon segment equation

        double determinant = a1*b2 - a2*b1;

        if (determinant != 0) // The lines are not parallel
        {
            double x = (b2*c1 - b1*c2)/determinant;
            double y = (a1*c2 - a2*c1)/determinant;
            vector<double> intersection_point = {x,y};
            bool ans = point_in_line(segment2,intersection_point);
            if (ans == true)
            {
                return true;
            }
        }
    }
    return false;
}

You May Also Enjoy